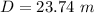Answer:
a
The height is
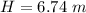
b
The horizontal distance is
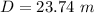
Step-by-step explanation:
From the question we are told that
The speed is
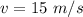
The angle is
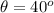
The height of the cannon from the ground is h = 2 m
The distance of the net from the ground is k = 1 m
Generally the maximum height she reaches is mathematically represented as
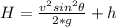
=>
![H = ((15)^2 [sin (40)]^2 )/(2 * 9.8) + 2](https://img.qammunity.org/2021/formulas/physics/high-school/m9sj4ynav0yq9y5efxq0scmrx62k9zb966.png)
=>
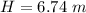
Generally from kinematic equation
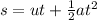
Here s is the displacement which is mathematically represented as
s = [-(h-k)]
=> s = -(2-1)
=> s = -1 m
There reason why s = -1 m is because upward motion canceled the downward motion remaining only the distance of the net from the ground which was covered during the first half but not covered during the second half
a = -g = -9.8
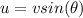
So
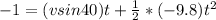
=>
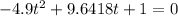
using quadratic formula to solve the equation we have
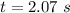
Generally distance covered along the horizontal is
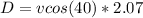
=>
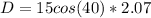
=>