Question

A toy box contains eight green balls and four purple balls. Suppose you choose a ball at random and then replace it by putting it back in the toy box. You then choose a second ball. What is the probability that you have selected a green ball and then a purple ball?

Option A: 2/9
Option B: 1/2
Option C: 1/3
Option D: 2/3

Answer 1

2/9

Explanation:

PJ= PG * PP = 2/3 * 1/3 = 2/9

Answer 2

Answer: C.
`(1)/(3)`

Explanation:

Given: Box contains 8 green balls and 4 purple balls.

Total balls = 8+4 = 12

event 1 = first picking green ball

event 2 = second picking purple balls.

As first ball was replaced, that means both events are independent.

Probability that you have selected a green ball and then a purple ball = P(purple ball )

Formula for probability =
`\frac{\text{favorable outcomes}}{\text{total outcomes}}`

Probability of selecting a purple ball (second pick)=
`(4)/(12)`

`=(1)/(3)`

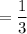
The required probability
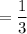`=(1)/(3)`, so C is correct option.