Question

The Apollo Lunar Module was used to make the transition from the spacecraft to the Moon's surface and back. Consider a similar module for landing on the surface of Mars. Use conservation of mechanical energy to answer these questions. (a) As the lander is descending, if the pilot decides to shut down the engine when the lander is at a height of 1.8 m, (this may not be a safe height to shut down the engine) and the velocity of the lander (relative to the surface of the planet) is 1.2 m/s what will be velocity of the lander at impact

Answer 1

v=6.05 m/s

Step-by-step explanation:

Given that,

Th initial velocity of the lander, u = 1.2 m/s

The lander is at a height of 1.8 m, d = 1.8 m

We need to find the velocity of the lander at impact. It is a concept based on the conservation of mechanical energy. So,

`(1)/(2)mv^2-(1)/(2)mu^2=W\\\\(1)/(2)mv^2-(1)/(2)mu^2=F* d\\\\(1)/(2)mv^2-(1)/(2)mu^2=mgd\\\\(1)/(2)m(v^2-u^2)=mgd\\\\v^2-u^2=2gd`

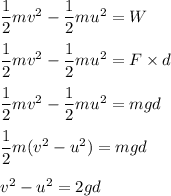
v is the velocity of the lander at the impact

g is the acceleration due to gravity on the surface of Mars, which is 0.4 times that on the surface of the Earth, g = 0.4 × 9.8 = 3.92 m/s²

So,

`v=√(u^2+2gd) \\\\v=√((1.2)^2+2* 9.8* 1.8) \\\\v=6.05\ m/s`

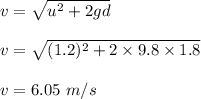
So, the velocity of the lander at the impact is 6.05 m/s.