Answer:
C. The solution t = 5 is the only valid solution to this system since time cannot be negative.
Explanation:
Given
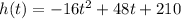
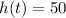
Required
Determine which of the options is true
After solving
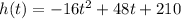
for
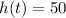
We have that
 and
and
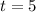
Because time can't be negative, we have to eliminate

So, we're left with
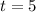
Because of this singular reason, we can conclude that option c answers the question