Answer:
Explanation:
a) This is a binomial distribution.
p = probability it is defective = 3% = 0.03, q = 1 - p = 1 - 0.03 = 0.97
This is a binomial distribution is given by the formula:

But n = 70
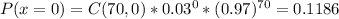
b) n = 102. Hence there can be 2 defective components, hence:
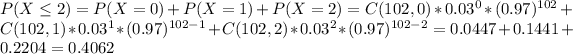
c) n = 105, there can be 5 defective products:
