Given:
The graph of
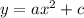 contains the point (2, 14).
contains the point (2, 14).
To find:
The point which lies on the graph of
 .
.
Solution:
Consider the given equations are
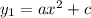 ...(i)
...(i)
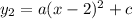 ...(ii)
...(ii)
The translation is defined as
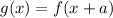
where, a is horizontal shift.
If a>0, then the graph shifts a units left and if a<0, then the graph shifts a units right.
From equation (i) and (ii), it is clear that a=-2. So, graph of
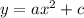 shifts 2 units right to get the graph of
shifts 2 units right to get the graph of
 .
.
It means each point on
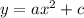 shifts 2 units right.
shifts 2 units right.

(2, 14) lies on
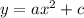 .
.
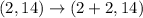
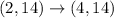
Therefore, (4,14) must be lies on
 .
.