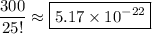See the link in comments (or if it gets deleted, look up "partial derangement"). The number of ways in which exactly
 items from a pool of
items from a pool of
 items can be rearranged such that only these
items can be rearranged such that only these
 items are in their original positions is
items are in their original positions is

where
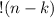 is the so-called sub-factorial that satisfies the relation
is the so-called sub-factorial that satisfies the relation
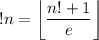
and
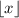 denotes the floor or greatest integer function of
denotes the floor or greatest integer function of
 , i.e. the greatest integer smaller than or equal to
, i.e. the greatest integer smaller than or equal to
 .
.
There are 25! ways of handing back exams with no extra constraint.
There are
 ways of handing back 23 exams to their original owners and 2 exams otherwise, and
ways of handing back 23 exams to their original owners and 2 exams otherwise, and
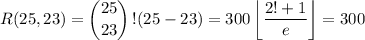
Then the probability of returning 23 exams correctly and 2 exams swapped is