Question

The function LaTeX: f\left(x\right)=-x^2+4f ( x ) = − x 2 + 4 defined on the interval LaTeX: -8\le x\le8− 8 ≤ x ≤ 8 is increasing on the interval LaTeX: \left[A,B\right][ A , B ] and decreasing on the interval LaTeX: \left[C,D\right][ C , D ]. Fill in the blanks below.

Answer 1

Given:

The function is

`f(x)=-x^2+4`

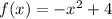
It defined on the interval -8 ≤ x ≤ 8.

To find:

The intervals on which the function is increasing and the interval on which decreasing.

Explanation:

We have,

`f(x)=-x^2+4`

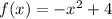
Differentiate with respect to x.

`f'(x)=-(2x)+(0)`

`f'(x)=-2x`

For turning point f'(x)=0.

`-2x=0`

`x=0`

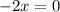
Now, 0 divides the interval -8 ≤ x ≤ 8 in two parts [-8,0] and [0,8]

For interval [-8,0], f'(x)>0, it means increasing.

For interval [0,8], f'(x)<0, it means decreasing.

Therefore, the function is increasing on the interval [-8,0] and decreasing on the interval [0,8].