Answer:
Considering the first statement
Standard deviation is resistive to unusual values
This statement is false because standard deviation is the numeric measure of deviation of the each observation from the mean
Considering the second statement
The standard deviation of a set of values is equal to 0 if and only if all of the values are the same.
This statement is true because standard deviation is the numeric measure of deviation of the each observation from the mean.
Considering the third statement
Standard deviation is never negative.
This statement is true because standard deviation is the numeric measure of deviation of the each observation from the mean.
Considering the fourth statement
Changing the units of a set of values (e.g., converting from inches to feet) does not affect its standard deviation
This statement is false because standard deviation is the numeric measure of deviation of the each observation from the mean
Considering the fifth statement
If a set of values has a mean of 0 and a standard deviation that is not 0, then adding a new data point with a value of 0 will have no effect on the standard deviation.
This statement is false because , let take an example
x -4 - 3 0 3 4
Generally the mean is mathematically evaluated as
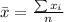
=>
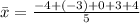
=>
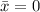
Generally the standard deviation is mathematically evaluated as
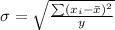
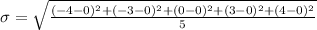
=>
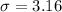
Now when zero is removed the standard deviation is
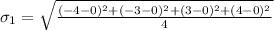
=>
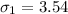
Since
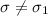 the above statement is false
the above statement is false
Considering the sixth statement
Standard deviation represents how far a group of values are from the mean of those values, on average.
This statement is true because standard deviation is the numeric measure of deviation of the each observation from the mean.
Explanation: