Question

Cos(100)-cos(99)=?
Can you do it step by step

Answer 1

Let's see what to do buddy...

________________________________

If 99 & 100 are in Degree

_________________________________

STEP (1)

The angles 99 and 100 are in the second quarter of the trigonometric circle.

The cosine is negative in the second quarter.

To make things easier, we can use angle conversion.

Look :

`we \: know \: that \: 100 = 90 + 10`

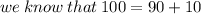
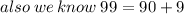
`also \: we \: know \: 99 = 90 + 9`

So :

`\cos(100) = \cos(90 + 10) = \cos( (\pi)/(2) + 10 ) \\`

`\cos(99) = \cos(90 + 9) = \cos( (\pi)/(2) + 9 ) \\`

_________________________________

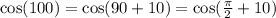
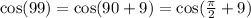
STEP (2)

Well now we have to do the arc deletion.

To remove the arc, we remove π/2 from the arc.

Remember that every time we remove π/2 from the arc, the trigonometric ratio changes.

That is, if it is a sine, it becomes a cosine, and if it is a cosine, it becomes a sine.

Or if it is a tangent, it becomes a cotangent, and if it is a cotangent, it becomes a tangent.

`in \: second \: quarter \: cosine \: is \: negative \\ \\ \cos( (\pi)/(2) + 10 ) = - \sin(10) = - 0.173`

`\cos( (\pi)/(2) + 9 ) = - \sin(9) = - 0.156 \\`

_________________________________

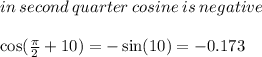
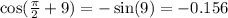
STEP (3)

`\cos(100) - \cos(99) = \\ - \sin(10) - ( - \sin(9) \: ) = \\ - 0.173 - ( - 0.156) = \\ - 0.173 + 0.156 = - 0.017`

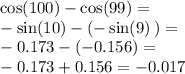
And we're done here.

_________________________________

If 99 & 100 are in Radian

_________________________________

STEP (1)

First we need to know how many degrees 1 radian is.

The following equation is used to convert degrees to radians or radians to degrees.

`(degree)/(180) = (radian)/(\pi) \\`

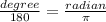
So we have :

`(d)/(180) = (1)/(\pi) \\`

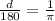
Multiply the sides of the equation by 180 :

`d = (180)/(\pi) = (180)/(3.14) = 57.32 \\`

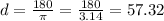
So 1 radian is approximately equal to 57 degrees.

And we have :

`100 \: rad \: = 100 * 57 = 5700 \: deg \\ \\ 99 \: rad \: = 99 * 57 = 5601 \: deg`

_________________________________

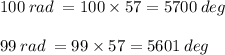
STEP (2)

Let's move on to deletion.

Look : 5700° = 15 × 360° + 300°

and : 5601° = 15 × 360° + 201°

We know π rad = 3.14 × 57 = 180° deg

So 2π rad = 2 × 180 = 360 ° deg

Then :5700 = 15 × 2 π + 300° = 30 π + 300°

and :5601 = 15 × 2 π + 201° = 30 π + 201°

Remember that deleting 2π is unconditional.

`\cos(30\pi + 300) = \cos(300) = \cos(360 - 60) = \cos(2\pi - 60) = \cos( - 60) = \\ cosine \: eat \: negative \\ \cos( - 60) = \cos(60) = (1)/(2)`

`\cos(30\pi + 201) = \cos(201) = \\ \cos(180 + 21) = \cos(\pi + 21) = \\ - \cos(21) = - 0.933`

`(1)/(2) - ( - 0.933) = 0.500 + 0.933 = 1.433`

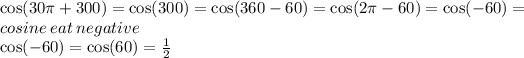
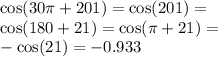
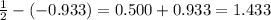
And we're done.

Thanks for watching buddy good luck.

♥️♥️♥️♥️♥️