Question

Triangle ABC is rotated 90 degrees clockwise about the origin to create triangle A'B'C'.

Triangle A,B,C with vertices at A(negative 3, 6), B(2, 9), and C(1, 1)

Answer 1

Note: Consider we need to find the vertices of the triangle A'B'C'

Given:

Triangle ABC is rotated 90 degrees clockwise about the origin to create triangle A'B'C'.

Triangle A,B,C with vertices at A(-3, 6), B(2, 9), and C(1, 1).

To find:

The vertices of the triangle A'B'C'.

Solution:

If triangle ABC is rotated 90 degrees clockwise about the origin to create triangle A'B'C', then

`(x,y)\to (y,-x)`

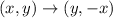
Using this rule, we get

`A(-3,6)\to A'(6,3)`

`B(2,9)\to B'(9,-2)`

`C(1,1)\to C'(1,-1)`

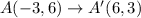
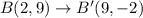
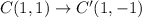
Therefore, the vertices of A'B'C' are A'(6,3), B'(9,-2) and C'(1,-1).