Note: Consider we need to find the vertices of the triangle A'B'C'
Given:
Triangle ABC is rotated 90 degrees clockwise about the origin to create triangle A'B'C'.
Triangle A,B,C with vertices at A(-3, 6), B(2, 9), and C(1, 1).
To find:
The vertices of the triangle A'B'C'.
Solution:
If triangle ABC is rotated 90 degrees clockwise about the origin to create triangle A'B'C', then
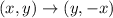
Using this rule, we get
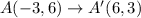

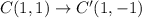
Therefore, the vertices of A'B'C' are A'(6,3), B'(9,-2) and C'(1,-1).