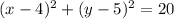Question

Find the equation of the circle with center (4,5) which passes through the y-intercept of the line 5x-2y+6=0​

Answer 1

(x-4)^2 + (y-5)^2 = 20

Explanation:

Rearrange the line equation of 5x - 2y + 6 = 0

So y = 5/2x +3

The y-intercept of the line equation is 3 as when x=0, y=3.

We know the Circle has the formula
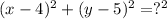`(x-4)^2 + (y-5)^2 = ?^2` from the question but with the intercept, we can find the entire equation as the y-intercept is (0,3) so we can substitute it into the equation to find the full equations so:

`(0-4)^2 + (3-5)^2 = ?^2`

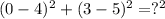
This simplifies to:

`(-4)^2 +(-2)^2` =
`?^2`

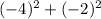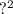
16 + 4 = 20 =
`?^2`

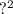
The answer is 20 so the equation of the circle is
`(x-4)^2 + (y-5)^2 = 20`