Question

How do I do this question?The aluminum cup inside your calorimeter weighs 39.78 g. You add 50.01 g of ice cold water to the calorimeter. You measure the temperature of the calorimeter to be 0.5oC just before your next addition. You then add 50.72 g of hot water and a 49.98 g metal object, all having an initial temperature of 69.5oC. After the calorimeter reaches thermal equilibrium, the final temperature is measured to be 35.9oC.

What is the specific heat of the metal object, in units of J g-1 oC-1.

Assume that:

the calorimeter is completely insulated
the heat capacity of the empty calorimeter is the heat capacity of the aluminum cup: 0.903 J g-1 oC-1.
the density of water is: 1.00 g/mL.
the heat capacity of water is: 4.184 J g-1 oC-1.
Perform all calculations without rounding, but then provide your answer to the correct number of significant figures. Units can be entered as J/(gK)

Answer 1

`Cp_(metal)=0.922(J)/(g\°C)`

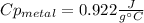
Step-by-step explanation:

Hello.

In this problem we must realize that there is heat flow that moves from the hot metal object and the hot water to the cold water and the cold aluminum cup, which allows us to write:

`Q_(cup)+Q_(cold,w)=-(Q_(metal)+Q_(hot,w))`

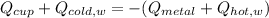
Which means that the heat lost be the hot metal object and the hot water is gained by both the cold water and the cold aluminum cup, which can be written in terms of mass, specific heats and change in temperature towards the equilibrium temperature (35.9 °C):

`m_(cup)Cp_(cup)(T_(eq)-T_(cup))+m_(cold,w)Cp_(cold,w)(T_(eq)-T_(cold,w))=-(m_(metal)Cp_(metal)(T_(eq)-T_(metal))+m_(hot,w)Cp_(hot,w)(T_(eq)-T_(hot,w))`

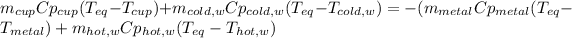
We need to solve for the specific heat of the metal as shown below:

`Cp_(metal)=(m_(cup)Cp_(cup)(T_(eq)-T_(cup))+m_(cold,w)Cp_(cold,w)(T_(eq)-T_(cold,w))+m_(hot,w)Cp_(hot,w)(T_(eq)-T_(hot,w)))/(-m_(metal)(T_(eq)-T_(metal))) \\\\Cp_(metal)=(39.78g*0.903(J)/(g\°C)(35.9-0.5)\°C+50.01g*4.184(J)/(g\°C)(35.9-0.5)\°C +50.72g*4.184(J)/(g\°C)(35.9-69.5)\°C )/(-49.98g(35.9-69.5)\°C ) \\\\Cp_(metal)=(1271.6J+7407.2J-7130.3J)/(-1679.3g\°C) \\\\Cp_(metal)=0.922(J)/(g\°C)`Best regards.