Question

Steam at 20 bars is in the saturated vapor state (call this state 1) and contained in a pistoncylinderdevice with a volume of 0.03 m3. Assume the steam is cooled at constantvolume (i.e. the piston is held fixed in place) until the temperature reaches 200 C (callthis state 2). Then the steam is expanded isothermally until its volume is three times theinitial value (state 3).

Required:
a. Determine the pressures at state 2 and 3. ans. 15.5 bar, ~10 bar
b. Determine the change in specific internal energy, u, for each of the two processes.
-389 kJ/kg, 410 kJ/kg
c. Make qualitatively correct sketches of the processes on a T-v plot.

Answer 1

Step-by-step explanation:

Given that:

At state 1:

Pressure P₁ = 20 bar

Volume V₁ = 0.03
`\mathbf{m^(3)}`

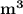
From the tables at saturated vapour;

Temperature T₁ = 212.4⁰ C ;
`v_1 = vg_1` = 0.0996
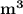`\mathbf{m^(3)}` / kg

The mass inside the cylinder is m = 0.3 kg, which is constant.

The specific internal energy u₁ = ug₁ = 2599.2 kJ/kg

At state 2:

Temperature T₂ = 200⁰ C

Since the 1 - 2 occurs in an isochoric process v₂ = v₁ = 0.099
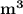`\mathbf{m^(3)}` / kg

From temperature T₂ = 200⁰ C

`v_f_2 = 0.0016 \ m^3/kg`

`vg_2 = 0.127 \ m^3/kg`

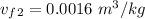
Since
`vf_2 < v_2<vg_2` , the saturated pressure at state 2 i.e. P₂ = 15.5 bar

Mixture quality
`x_2 = (v_2-vf_2)/(vg_2 -vf_2)`

`x_2 = ((0.099-0.0016)m^3/kg)/((0.127 -0.0016) m^3/kg)`

`x_2 = ((0.0974)m^3/kg)/((0.1254) m^3/kg)`

`\mathsf{x_2 =0.78}`

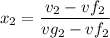
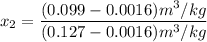
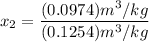
At temperature T₂, the specific internal energy
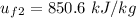`u_f_2 = 850.6 \ kJ/kg` , also
`ug_2 = 2594.3 \ kJ/kg`

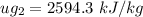
Thus,

`u_2 = uf_2 + x_2 (ug_2 -uf_2)`

`u_2 =850.6 +0.78 (2594.3 -850.6)`

`u_2 =850.6 +1360.086`

`u_2 =2210.686 \ kJ/kg`

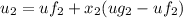
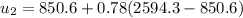
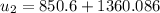
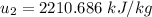
At state 3:

Temperature
`T_3=T_2 = 200 ^0 C ,`

`V_3 = 2V_1 = 0.06 \ m^3`

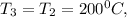
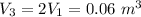
Specific volume
`v_3 = 0.2 \ m^3/kg`

Thus;
`vg_3 =vg_2 = 0.127 \ m^3/kg` ,

SInce
`v_3 > vg_3`, therefore, the phase is in a superheated vapour state.

From the tables of superheated vapour tables; at
`v_3 = 0.2 \ m^3/kg` and T₃ = 200⁰ C

The pressure = 10 bar and v =0.206
`\ m^3/kg`

The specific internal energy
`u_3` at the pressure of 10 bar = 2622.3 kJ/kg

The changes in the specific internal energy is:

`u_2-u_1`

= (2210.686 - 2599.2) kJ/kg

= -388.514 kJ/kg

≅ - 389 kJ/kg

`u_3-u_2`

= (2622.3 - 2210.686) kJ/kg

= 411.614 kJ/kg

≅ 410 kJ/kg

We can see the correct sketches of the T-v plot showing the diagrammatic expression in the image attached below.