Question

Photos and videos have become an important part of the online social experience, with more than half of Internet users posting photos or videos online that they have taken themselves. Let A be the event an Internet user posts photos that they have taken themselves, and B be the event an Internet user posts videos that they have taken themselves. A research center finds that P(A) = 0.47, P(B) = 0.28,and P(A or B) = 0.52.

Required:
What is the conditional probability that an Internet user posts photos that they have taken themselves, given that they post videos that they have taken themselves?

Answer 1

0.82

Explanation:

Given:

A be the event that an Internet user posts photos taken by themselves.

B be the event that an Internet user posts photos taken by themselves.

P(A) = 0.47

P(A) = 0.28

P(A or B) =
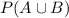`P(A\cup B)` = 0.52

To find:

Conditional probability that an Internet user posts photos given that they post videos.

OR

P(A/B) = ?

Solution:

Formula to be used to find the required conditional probability:

`P(A/B) = (P(A \cap B))/(P(B))`

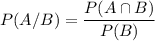
For this,
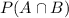`P(A \cap B)` is required.

Formula

`P(A \cup B) = P(A) + P(B) - P(A \cap B)`

`0.52=0.47+0.28-P(A\cap B)\\\Rightarrow P(A\cap B)=0.23`

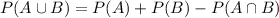
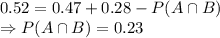
Now, the required conditional probability is:

`P(A/B) = (P(A \cap B))/(P(B))\\\Rightarrow P(A/B) = (0.23)/(0.28)\\\Rightarrow \bold{P(A/B)} = 0.82}`

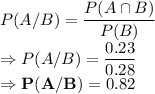
So, the answer is 0.82.