Answer:
0.82
Explanation:
Given:
A be the event that an Internet user posts photos taken by themselves.
B be the event that an Internet user posts photos taken by themselves.
P(A) = 0.47
P(A) = 0.28
P(A or B) =
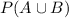 = 0.52
= 0.52
To find:
Conditional probability that an Internet user posts photos given that they post videos.
OR
P(A/B) = ?
Solution:
Formula to be used to find the required conditional probability:
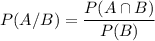
For this,
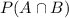 is required.
is required.
Formula
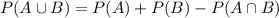
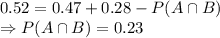
Now, the required conditional probability is:
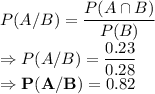
So, the answer is 0.82.