Answer:
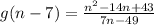 → (a)
→ (a)
Explanation:
We need to evaluate g(n - 7), where
Replace x by (n - 7) to evaluate it
∵ x = (n - 7)
∴
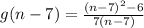
→ Let us find (n - 7)²
∵ (n - 7)² = (n - 7)(n - 7) = (n)(n) + (n)(-7) + (-7)(n) + (-7)(-7)
∴ (n - 7)² = n² + (-7n) + (-7n) + 49 = n² + -14n + 49
∴ (n - 7)² = n² - 14n + 49
→ Find 7(n - 7)
∵ 7(n - 7) = 7(n) - 7(7)
∴ 7(n - 7) = 7n - 49
→ Now let us write then in the form above
∵
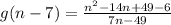
→ Add the like terms in the numerator
∴
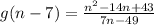
The correct answer is (a)