Question

Functions and their Properties

Practice
Need help​

Answer 1

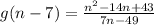`g(n-7)=(n^(2)-14n+43)/(7n-49)` → (a)

Explanation:

We need to evaluate g(n - 7), where

• 
  `g(x)=(x^(2)-7)/(7x)`

Replace x by (n - 7) to evaluate it

∵ x = (n - 7)

∴
`g(n-7)=((n-7)^(2)-6)/(7(n-7))`

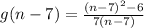
→ Let us find (n - 7)²

∵ (n - 7)² = (n - 7)(n - 7) = (n)(n) + (n)(-7) + (-7)(n) + (-7)(-7)

∴ (n - 7)² = n² + (-7n) + (-7n) + 49 = n² + -14n + 49

∴ (n - 7)² = n² - 14n + 49

→ Find 7(n - 7)

∵ 7(n - 7) = 7(n) - 7(7)

∴ 7(n - 7) = 7n - 49

→ Now let us write then in the form above

∵
`g(n-7)=(n^(2)-14n+49-6)/(7n-49)`

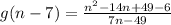
→ Add the like terms in the numerator

∴
`g(n-7)=(n^(2)-14n+43)/(7n-49)`

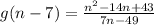
The correct answer is (a)