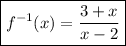Question

Find the inverse of f(x)= 2x+3/x-1

Answer 1

`\displaystyle f^(-1)(x)=(3+x)/(x-2)`

Explanation:

We have the function:

`\displaystyle f(x)=(2x+3)/(x-1)`

Find the inverse of f(x). First, we call y=f(x):

`\displaystyle y=(2x+3)/(x-1)`

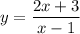
We have to solve for x. Multiply by x-1:

`y(x-1)=2x+3`

Operate:

`yx-y=2x+3`

Join all the x's to the left side and move the rest to the right side:

`yx-2x=3+y`

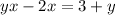
Factor:

`x(y-2)=3+y`

Solve for x:

`\displaystyle x=(3+y)/(y-2)`

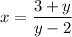
Interchange the variables:

`\displaystyle y=(3+x)/(x-2)`

This is the inverse function:

`\boxed{\displaystyle f^(-1)(x)=(3+x)/(x-2)}`