Answer:

Explanation:
In order to find the value of x and y in this, we have to note a couple of angle relationships.
We know that angles
 and
and
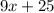 are the same because they are corresponding angles. This means that when a line intersects two parallel lines, the angles formed are congruent to the second line.
are the same because they are corresponding angles. This means that when a line intersects two parallel lines, the angles formed are congruent to the second line.
This means both expressions for the line will be equal to each other:
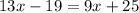
We can now solve for x.
Add 19 to both sides:
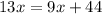
Subtract 9x from both sides:
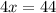
Divide both sides by 4:
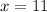
Now that we know that x = 11, we can use another angle relationship to find y.
We know that
 and
and
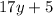 are supplementary angles. This means their angle measurements add up to 180°.
are supplementary angles. This means their angle measurements add up to 180°.
Since we know the value of x, we can find the measure of the angle
 .
.

So the
 angle is equal to 124 degrees. Since this and
angle is equal to 124 degrees. Since this and
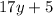 are supplementary, that means
are supplementary, that means
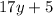 must be equal to
must be equal to
 degrees.
degrees.

Subtract 5 from both sides:
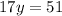
Divide both sides by 17:
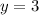
So, x = 11 and y = 3.
Hope this helped!