Answer:
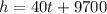
where the elevation, h, is in feet and time, t, is in minutes.
Explanation:
At the time,
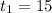 min, the elevation,
min, the elevation,
 feet and
feet and
at the time
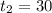 min, the elevation,
min, the elevation,
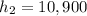 feet.
feet.
As they are hiking a steady incline, so the change in the elevation with respect to time will be constant.
So, there will be a linear relationship between the elevation and the time.
Let
 be the elevation at any time instant
be the elevation at any time instant
 , so the linear relation among these quantities is
, so the linear relation among these quantities is
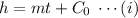
where
 is the rate of change of elevation with respect to time and
is the rate of change of elevation with respect to time and
 is constant.
is constant.
The change in the elevation,
 feet.
feet.
and the change in time,
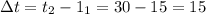 min.
min.
So, change in the elevation in unit time,
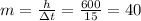 feet/min.
feet/min.
Now, from equation (i)
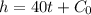
As the elevation,
 at time
at time
 , so
, so
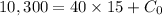

Hence, the required equation is
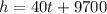
where the elevation,
 , is in feet and time,
, is in feet and time,
 , is in minutes.
, is in minutes.