Answer:
a) v = 7.28 m/s
b) t = 0.74 s
Step-by-step explanation:
a) The initial speed of the ball can be calculated using the following equation:
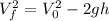
Where:
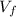 is the final speed = 0
is the final speed = 0
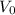 is the initial speed =?
is the initial speed =?
g: is the gravity = 9.81 m/s²
h: is the height = 2.70 m
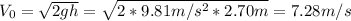
Hence, the initial speed of the ball is 7.28 m/s.
b) To find the time that takes the balls to reach the ceiling we can use the next equation:
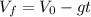
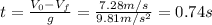
Therefore, the time it takes for the ball to reach the ceiling is 0.74 s.
I hope it helps you!