Answer:
The 80% confidence interval for the average net change in a student's score after completing the course is (15.4, 26.3).
Explanation:
The net change in 7 students' scores on the exam after completing the course are:
S = {37 ,12 ,12 ,17 ,13 ,32 ,23}
Compute the sample mean and sample standard deviation as follows:
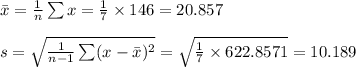
As the population standard deviation is not known, a t-interval will be formed.
Compute the critical value of t for 80% confidence interval and 6 degrees of freedom as follows:

*Use a t-table.
Compute the 80% confidence interval for the average net change in a student's score after completing the course as follows:


Thus, the 80% confidence interval for the average net change in a student's score after completing the course is (15.4, 26.3).