Question

A certain test preparation course is designed to help students improve their scores on the MCAT exam. A mock exam is given at the beginning and end of the course to determine the effectiveness of the course. The following measurements are the net change in 7 students' scores on the exam after completing the course: 37,12,12,17,13,32,23 Using these data, construct a 80% confidence interval for the average net change in a student's score after completing the course. Assume the population is approximately normal. Step 1 of 4 : Calculate the sample mean for the given sample data. Round your answer to one decimal place.

Answer 1

The 80% confidence interval for the average net change in a student's score after completing the course is (15.4, 26.3).

Explanation:

The net change in 7 students' scores on the exam after completing the course are:

S = {37 ,12 ,12 ,17 ,13 ,32 ,23}

Compute the sample mean and sample standard deviation as follows:

`\bar x=(1)/(n)\sum x=(1)/(7)* 146=20.857\\\\s=\sqrt{(1)/(n-1)\sum (x-\bar x)^(2)}}=\sqrt{(1)/(7)* 622.8571}=10.189`

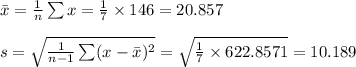
As the population standard deviation is not known, a t-interval will be formed.

Compute the critical value of t for 80% confidence interval and 6 degrees of freedom as follows:

`t_(\alpha/2, (n-1))=t_(0.20/2, (7-1))=t_(0.10,6)=1.415`

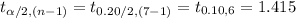
*Use a t-table.

Compute the 80% confidence interval for the average net change in a student's score after completing the course as follows:

`CI=\bar x\pm t_(\alpha/2, (n-1))*(s)/(√(n))`

`=20.857\pm 1.415*(10.189)/(√(7))\\\\ =20.857\pm 5.4493\\\\=(15.4077, 26.3063)\\\\\approx (15.4,26.3)`

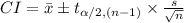
Thus, the 80% confidence interval for the average net change in a student's score after completing the course is (15.4, 26.3).