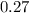Answer:
The expected no. of shortage will be "0.27".
Step-by-step explanation:
The given values are:
Ordering cost,
O = $250
Holding cost (i),
= 1% (per week)
= 52% (a year)
Cost of goods (C),
= $2.75
The average annual demand is:

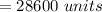
Now,
⇒
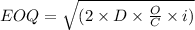
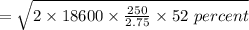
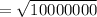
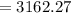
In a year, the number of orders will be:
⇒
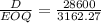
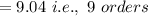
Demand mean will be:
=

=

=
![max[((Upper \ limit - Mean))/(3) , ((mean-lower \ limit))/(3) ]](https://img.qammunity.org/2021/formulas/business/college/bsdoucbiw1jpp2zyhkxrhk318mcj2yxiwc.png)
=
![max [(50)/(3) ,(50)/(3) ]](https://img.qammunity.org/2021/formulas/business/college/nezd52axkoxwv8p952r86djhri142kshub.png)
=
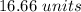
So, in a year, the expected number of the shortages will be:
⇒
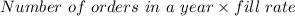
⇒

⇒