Question

Determine an interest rate less than 15%, a period of investment greater than two years, and a regular payment that will result in the total amount of interest you earn being equal to the total amount of money you put in?for example, under what conditions will you have a future value of $1 000 000, having earned $500 000 interest?)

Answer 1

It will take 5.29 years to double our money if we invest $500 at 14 percent interest.

Step-by-step explanation:

Let we invest $500 with the interest rate of 14% ,

Now we will find the time it is going to take to double the money

here, we use the formula of compound interest
`A= P( 1+(r)/(n)) ^(nt)`

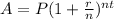
Here, A = the amount yielded,

P = principal,

r = interest rate ,

n = number of times per year,

and t = time invested.

Now, put A= 1000 , P= 500 , R= 0.14 T= x and N= 1

`1000=500(1+ 0.14)^x`

`1000=500(1.14)^x`

`2=1.14^x`

`\log_(1.14) (2)=x`

`x=5.29`

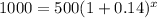
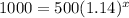
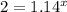
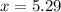
so , It will take 5.29 years to double our money if we invest $500 at 14 percent interest.

Hence , the answer is 5.29 years .