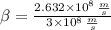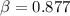Answer:
a)
 , b)
, b)
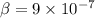 , c)
, c)
 , d)
, d)
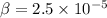 , e)
, e)
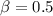 , f)
, f)
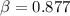
Step-by-step explanation:
From relativist physics we know that
 is the symbol for the speed of light, which equal to approximately 300000 kilometers per second. (300000000 meters per second).
is the symbol for the speed of light, which equal to approximately 300000 kilometers per second. (300000000 meters per second).
a) A car traveling 120 kilometers per hour:
At first we convert the car speed into meters per second:

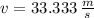
The ratio
 is now calculated: (
is now calculated: (
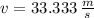 ,
,
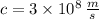 )
)
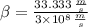

b) A commercial jet airliner traveling 270 meters per second:
The ratio
 is now calculated: (
is now calculated: (
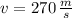 ,
,
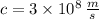 )
)

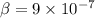
c) A supersonic airplane traveling Mach 2.7:
At first we get the speed of the supersonic airplane from Mach's formula:
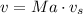
Where:
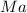 - Mach number, dimensionless.
- Mach number, dimensionless.
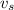 - Speed of sound in air, measured in meters per second.
- Speed of sound in air, measured in meters per second.
If we know that
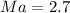 and
and
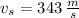 , then the speed of the supersonic airplane is:
, then the speed of the supersonic airplane is:

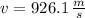
The ratio
 is now calculated: (
is now calculated: (
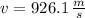 ,
,
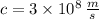 )
)
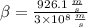

d) The space shuttle, travelling 27000 kilometers per hour:
At first we convert the space shuttle speed into meters per second:
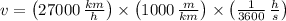
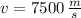
The ratio
 is now calculated: (
is now calculated: (
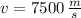 ,
,
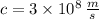 )
)
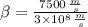
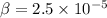
e) An electron traveling 30 centimeters in 2 nanoseconds:
If we assume that electron travels at constant velocity, then speed is obtained as follows:
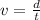
Where:
 - Speed, measured in meters per second.
- Speed, measured in meters per second.
 - Travelled distance, measured in meters.
- Travelled distance, measured in meters.
 - Time, measured in seconds.
- Time, measured in seconds.
If we know that
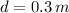 and
and
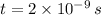 , then speed of the electron is:
, then speed of the electron is:
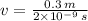

The ratio
 is now calculated: (
is now calculated: (
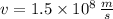 ,
,
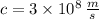 )
)
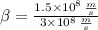
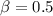
f) A proton traveling across a nucleus (10⁻¹⁴ meters) in 0.38 × 10⁻²² seconds:
If we assume that proton travels at constant velocity, then speed is obtained as follows:
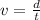
Where:
 - Speed, measured in meters per second.
- Speed, measured in meters per second.
 - Travelled distance, measured in meters.
- Travelled distance, measured in meters.
 - Time, measured in seconds.
- Time, measured in seconds.
If we know that
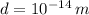 and
and
 , then speed of the electron is:
, then speed of the electron is:
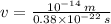
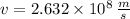
The ratio
 is now calculated: (
is now calculated: (
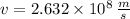 ,
,
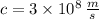 )
)