Question

Akiko wants to fence in her
`12` ft by
`10` ft vegetable garden. There will be a path
`x` ft wide between the garden and the fence. The area to be enclosed by the fence will be
`360` sq ft. Write a quadratic function that can be used to determine the value of
`x`.

Answer 1

see below

Explanation:

The length is 12 + 2x and the width is 10 + 2x

A = l*w

360 = ( 12+2x) ( 10+2x)

FOIL

360 = 120 + 24x+20x + 4x^2

Combine like terms

360 = 4x^2 +44x+120

Subtract 360 from each side

0 = 4x^2 +44x +120-360

0 = 4x^2+ 44x -240

For fun, lets solve

0 = 4( x^2 + 11x - 60)

0 = 4( x+15) ( x-4)

Using the zero product property

x= -15 x=4

Since we cannot have negative length

x=4 ft

Answer 2

`x^2+11x-60=0`

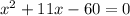
Explanation:

Refer to the drawing.

We know that the area enclosed by the fence is 360 square feet. Remember that the area for a rectangle is given by the following formula:

`A=bh`

So, let's substitute 360 for A, (12+2x) for b, and (10+2x) for h. This yields:

`360=(12+2x)(10+2x)`

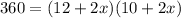
We can simplify this. On the right, factor out a 2 from the first term and a 2 from the second. This yields:

`360=2(6+x)\cdot2(5+x)`

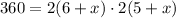
Multiply:

`360=4(x+6)(x+5)`

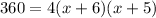
Divide both sides by 4:

`90=(x+6)(x+5)`

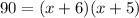
Multiply on the right:

`90=x^2+6x+5x+30`

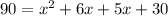
Add on the right:

`90=x^2+11x+30`

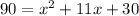
Subtract 90 from both sides. So, our equation is:

`x^2+11x-60=0`

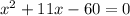
And we're done!