Answer:
The unit energy losses due to nonconservative forces is 881.40 joules per kilogram.
Step-by-step explanation:
We can estimate the unit energy losses of gas eruption by Principle of Energy Conservation and Work-Energy Theorem:
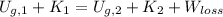 (Eq. 1)
(Eq. 1)
Where:
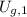 - Gravitational potential energy of gas eruptions at surface, measured in joules.
- Gravitational potential energy of gas eruptions at surface, measured in joules.
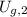 - Gravitational potential energy of gas eruptions at highest height, measured in joules.
- Gravitational potential energy of gas eruptions at highest height, measured in joules.
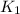 - Translational kinetic energy of gas eruptions at surface, measured in joules.
- Translational kinetic energy of gas eruptions at surface, measured in joules.
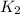 - Translational kinetic energy of gas eruptions at highest height, measured in joules.
- Translational kinetic energy of gas eruptions at highest height, measured in joules.
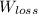 - Energy losses due to nonconservative forces, measured in joules.
- Energy losses due to nonconservative forces, measured in joules.
We clear the component associated with energy losses in (Eq. 1):
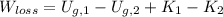
And we expand it afterwards:
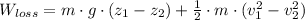 (Eq. 2a)
(Eq. 2a)
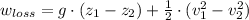 (Eq. 2b)
(Eq. 2b)
Where:
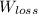 - Energy losses due to nonconservative forces, measured in joules.
- Energy losses due to nonconservative forces, measured in joules.
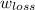 - Unit energy losses due to nonconservative forces, measured in joules per kilogram.
- Unit energy losses due to nonconservative forces, measured in joules per kilogram.
 - Gravitational acceleration, measured in meters per second.
- Gravitational acceleration, measured in meters per second.
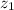 ,
,
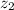 - Bottom and top height, measured in meters.
- Bottom and top height, measured in meters.
 ,
,
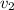 - Gas eruption speeds at surface and highest heights, measured in meters per second.
- Gas eruption speeds at surface and highest heights, measured in meters per second.
If we know that
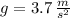 ,
,
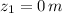 .
.
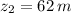 .
.
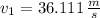 and
and
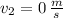 , the unit energy losses are:
, the unit energy losses are:
![w_(loss) = \left(3.7\,(m)/(s^(2)) \right)\cdot (62\,m-0\,m)+(1)/(2) \cdot \left[\left(36.11\,(m)/(s) \right)^(2)-\left(0\,(m)/(s) \right)^(2)\right]](https://img.qammunity.org/2021/formulas/physics/college/vc79isl4kwx9x5hnluy9i5x159v6sdxn6k.png)
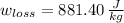
The unit energy losses due to nonconservative forces is 881.40 joules per kilogram.