Answer:
Yes there is a significant difference in the standard deviations of the two sets of measurements made by the two instruments at the 95%

Explanation:
From the question we are told that
The normal bicarbonate level is k = 23-29 mmol/L
The number of times the blood was tested is n = 6
The mean concentration for old instrument is
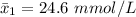
The standard deviation is

The mean concentration for the new instrument is
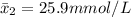
The standard deviation is
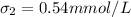
The confidence level is 95%
The level of significance is mathematically represented as


Generally the test statistics is mathematically represented as
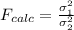
=>
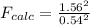
=>

Generally the degree of freedom for the old instrument is is mathematically evaluated as

=>
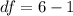
=>
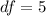
Generally the degree of freedom for the new instrument is is mathematically evaluated as
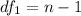
=>
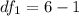
=>
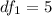
For the f distribution table the critical value of
 at df and
at df and
 is
is
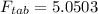
Generally given that the
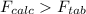 it means that there is a significant difference in the standard deviations of the two sets of measurements made by the two instruments at the 95%
it means that there is a significant difference in the standard deviations of the two sets of measurements made by the two instruments at the 95%