Answer:
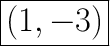
Explanation:
In order to find the solution to this system of equations, our goal is to get one variable on one side of the equation.
With the equations d
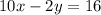 , and
, and
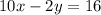 , we know that we can multiply
, we know that we can multiply
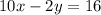 by -1 and the x terms will cancel out (as 10 - 10 = 0).
by -1 and the x terms will cancel out (as 10 - 10 = 0).
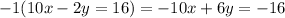
Now we add this equation to the first.

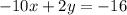
_______________

Divide both sides by 11 and we get
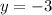 .
.
Now that we know the value of y, we can substitute it inside an equation and find the value of x. Let's substitute it inside
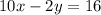 .
.

So x = 1.
Hope this helped!
Hope this helped!