Question

If 5(3x-1)=55 what is the value of 2x-2

Answer 1

Answer: 6

Explanation:

We first Solve for ‘x’ :-

=> 5(3x - 1) = 55
= 15x - 5 = 55
= 15x = 55 + 5 = 60
=> x = 60/15 = 4

Therefore, x = 4

We can now Substitute the value of ‘x’ in 2x - 2 to find the value :-

= 2x - 2
= 2(4) - 2
= 8 - 2
= 6

Therefore, 2x - 2 = 6 (as x = 4)

Answer 2

Hey ! there

Answer:

• Value of 2x - 2 is 6 .

Explanation:

In this question we are provided with an equation that is 5 ( 3x - 1 ) = 55 and we are asked to find the value of 2x - 2 .

Firstly , we need to find the value of x . So we need to solve the equation .

SOLUTION : -

`\quad \longmapsto \qquad \: 5(3x - 1) = 55`

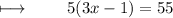
Step 1 : Dividing with 5 on both sides :

`\quad \longmapsto \qquad \: \frac{ \cancel{5}(3x - 1)}{ \cancel{5}} = \cancel{(55)/(5) }`

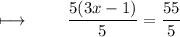
On cancelling , We get :

`\quad \longmapsto \qquad \:3x - 1 = 11`

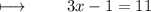
Step 2 : Adding 1 on both sides :

`\quad \longmapsto \qquad \:3x - \cancel{1} + \cancel{1} = 11 + 1`

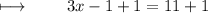
On simplifying , We get :

`\quad \longmapsto \qquad \:3x = 12`

Step 3 : Dividing with 3 on both sides :

`\quad \longmapsto \qquad \: \frac{ \cancel{3}x}{ \cancel{3}} = \cancel{ (12)/(3) }`

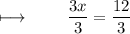
We get ,

`\quad \longmapsto \qquad \: \underline{\boxed{\frak{x = 4}}}`

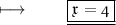
→ Therefore , value of x is 4 .

Verifying : -

Now we are verifying whether our answer is wrong or right . So ,

• 5 ( 3x - 1 ) = 55

• 5 { 3( 4 ) - 1 } = 55

• 5 ( 12 - 1 ) = 55

• 5 ( 11 ) = 55

• L.H.S = R.H.S

• Hence , Verified .

Therefore , our value of x is correct/valid .

We need to find the value of 2x - 2 .

`\quad \longmapsto \qquad \:2x - 2`

So substituting value of x in it :

`\quad \longmapsto \qquad \:2( \bold{4}) - 2`

Multiplying 2 with 4 :

`\quad \longmapsto \qquad \:8 - 2`

Subtracting 2 from 8 :

`\quad \longmapsto \qquad \: \blue{\underline{\boxed{\frak{6}}}} \quad \: \bigstar`

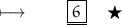
• Henceforth, value of 2x - 2 is ❝ 6 ❞.

#Keep Learning