Question

Daphne likes to ski at a resort that is open from December through April. According to a sign at the resort, 20, percent of the snow falls occur in December, 25, percent in January, 20, percent in February, 20, percent in March, and 15, percent in April. She wondered if the snow falls in her hometown followed this distribution, so she took a random sample of 80 days between December and April with snowfall and recorded their months. Here are her results:_______.

Month December January February March April
Days 16 11 16 18 19
She wants to use these results to carry out a x2 goodness-of-fit test to determine if the distribution of snowfalls in her hometown disagrees with the claimed percentages.

Answer 1

Answer:
x^2 = 8.383;

0.05 < P-value < 0.10

Explanation:

Answer 2

Explanation:

From the given information:

We can compute the null hypothesis & the alternative hypothesis as:

`{H_o}:\text{Distribution of snowfalls in her hometown is similar to claimed percentage }`

`{H_a}:\text{Distribution of snowfalls in her hometown is not similar to claimed percentage }`

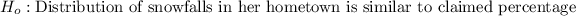
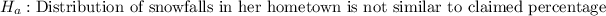
The degree of freedom = n - 1

The degree of freedom = 5 - 1

The degree of freedom = 4

At the level of significance of 0.05 and degree of freedom 4,

the rejection region = 9.488

However, we can compute the chi-square X² goodness of fit test as:

months frequency (p) observed O Expected E Chi-square
`X^2= ((O-E)^2)/(E)`

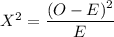
Dec 0.2 16 16
`((16-16)^2)/(16) =0`

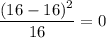
Jan 0.250 11 20
`((11-20)^2)/(20) =4.050`

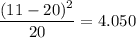
Feb 0.200 16 16
`((16-16)^2)/(16) =0`

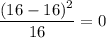
Mar 0.200 18 16
`((18-16)^2)/(16) =0.250`

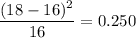
Apr 0.150 19 12
`((19-12)^2)/(12) =4.083`

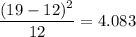
Total 1.000 80 80 8.3833

∴

The test statistics X² = 8.3833

Thus; we fail to reject the
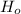`H_o` since test statistics X² doesn't fall in the rejection region.

Therefore; there is sufficient evidence to conclude that the distribution of snowfalls in her hometown is not similar to the claimed percentage.