Answer:
Explanation:
From the given information:
We can compute the null hypothesis & the alternative hypothesis as:
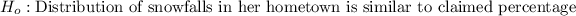
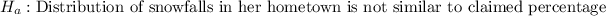
The degree of freedom = n - 1
The degree of freedom = 5 - 1
The degree of freedom = 4
At the level of significance of 0.05 and degree of freedom 4,
the rejection region = 9.488
However, we can compute the chi-square X² goodness of fit test as:
months frequency (p) observed O Expected E Chi-square
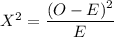
Dec 0.2 16 16
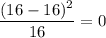
Jan 0.250 11 20
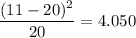
Feb 0.200 16 16
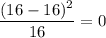
Mar 0.200 18 16
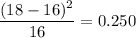
Apr 0.150 19 12
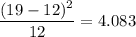
Total 1.000 80 80 8.3833
∴
The test statistics X² = 8.3833
Thus; we fail to reject the
 since test statistics X² doesn't fall in the rejection region.
since test statistics X² doesn't fall in the rejection region.
Therefore; there is sufficient evidence to conclude that the distribution of snowfalls in her hometown is not similar to the claimed percentage.