Question

The length of a rectangle is 3 ft longer than its width. The perimeter of the rectangle is 30 ft. Write an equation to represent the perimeter in terms of its width w. What is the length of the rectangle?

Answer 1

Explanation:

30=2(3)+2w

Answer 2

Let the width of the rectangle be w.

Let the length of the rectangle be l.

★ If the length is 3 feet longer than the width, then the length can be written in terms of the width as:

• l = w + 3

Now, the formula for finding the perimeter is p = 2l + 2w.

Substituting the values in this formula -

`\\ \implies \sf \: p = 2(w + 3) + 2w \\ \\ \\ \implies \sf \: p = 2w + 6 + 2w \\ \\ \\ \implies \sf \: p = 4w + 6 \\`

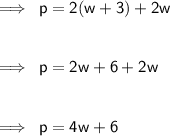
Substituting P = 30 for p ( allows us to solve for p) -

`\\ \implies \sf \: 30 = 4w + 6 \\ \\ \\ \implies \sf \: 30 - 6 = 4w + 6 - 6 \\ \\ \\ \implies \sf24 = 4w \\ \\ \\ \implies \sf \: w = (24)/(4) \\ \\ \\ \dag \: \large{ \underline{ \boxed{ \sf{ \: w = 6 \: cm}}}} \\`

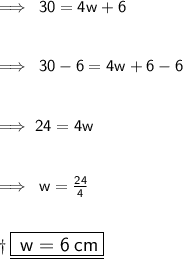
Substituting w = 6 for l in the equation l = w + 7 -

`\\ \implies \sf \: l = 6 + 7 \\ \\ \\ \implies \sf \blue{l = 13 \: cm}`