Answer:
x = 50.5° (3 sf)
Explanation:
Sine Rule for side lengths
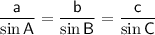
(where A, B and C are the angles and a, b and c are the sides opposite the angles)
Find BD:
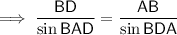
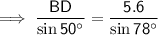
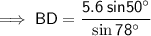
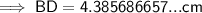
Angles on a straight line sum to 180°
⇒ ∠ADB + ∠BDC = 180°
⇒ 78° + ∠BDC = 180°
⇒ ∠BDC = 102°
Sine Rule for angles
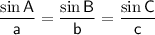
(where A, B and C are the angles and a, b and c are the sides opposite the angles)
Find ∠BCD:
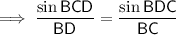
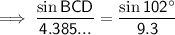
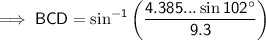
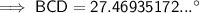
The interior angles of a triangle sum to 180°
⇒ ∠CBD + ∠BDC + ∠BCD = 180°
⇒ x + 102° + 27.469...° = 180°
⇒ x = 50.53064828...°
⇒ x = 50.5° (3 sf)