Question

I will give you 100 points HELp

Answer 1

CD ≈ 26.0 cm

Explanation:

using the sine ratio in right triangle ABD

sin35° =
`(opposite)/(hypotenuse)` =
`(AB)/(BD)` =
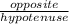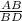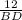`(12)/(BD)` ( multiply both sides by BD )

BD × sin35° = 12 ( divide both sides by sin35° )

BD =
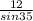`(12)/(sin35)` ≈ 20.92 cm

using the sine rule in Δ BCD

`(BD)/(sinC)` =
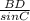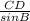`(CD)/(sinB)` , that is

`(20.92)/(sin52)` =
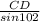`(CD)/(sin102)` ( cross- multiply )

CD × sin52° = 20.92 × sin102° ( divide both sides by sin52° )

CD =
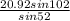`(20.92sin102)/(sin52)` ≈ 26.0 cm ( to 3 significant figures )

Answer 2

CD = 26.0 cm (3 sf)

Explanation:

Sine Rule for side lengths

`\sf (a)/(\sin A)=(b)/(\sin B)=(c)/(\sin C)`

(where A, B and C are the angles and a, b and c are the sides opposite the angles)

Find length BD:

`\implies \sf (AB)/(\sin ADB)=(BD)/(\sin BAD)`

`\implies \sf (12)/(\sin 35^(\circ))=(BD)/(\sin 90^(\circ))`

`\implies \sf BD=(12\sin 90^(\circ))/(\sin 35^(\circ))`

`\implies \sf BD=20.92136155...cm`

Find length CD:

`\implies \sf (BD)/(\sin BCD)=(CD)/(\sin DBC)`

`\implies \sf (20.921...)/(\sin 52^(\circ))=(CD)/(\sin 102^(\circ))`

`\implies \sf CD=(20.921...\sin 102^(\circ))/(\sin 52^(\circ))`

`\implies \sf CD=25.96941667...cm`

Therefore, CD = 26.0 cm (3 sf)