Answer: see proof below
Explanation:
Since (a, b) is equidistant from (-a, 2) and (2, -b), then it is the midpoint of the those two points. Use Midpoint formula to find (a, b).
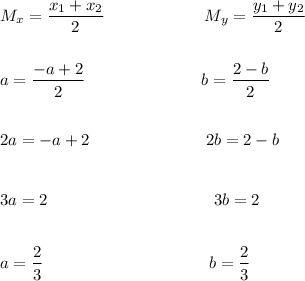
3(a + b) - 4 = 0
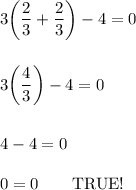
Notice that I changed the equation to "negative 4" because the equation you provided did not make a true statement.