Answer:
Alia=28
Huda=12
Explanation:
Let the constant of proportionality be x
Hence, no. of sweets Alia had initially = 7x
No. of sweets Huda had initially = 3x
No. of sweets Alia has now= 7x-3
No. of sweets Huda has now= 3x+3
We know that, the ratio of the no. of sweets Alia has now to no. of sweets Huda has now = 5:3
Hence,
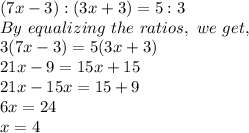
As we now got the constant of proportionality to be 4,
No. of sweets Alia had initially = 7*4=28
No. of sweets Huda had initially= 3*4=12