Answer:
A pythagorean identity means that for any angle
 ,
,
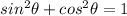 .
.
This also means
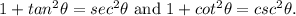 The symbol, theta (
The symbol, theta (
 ) represents one of the acute angles in the right triangle. The hypotenuse (familiarly c in the regular pythagorean theorem) is 1. The triangle base is
) represents one of the acute angles in the right triangle. The hypotenuse (familiarly c in the regular pythagorean theorem) is 1. The triangle base is
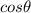 , and the height (side perpendicular to the base, making a right angle) is
, and the height (side perpendicular to the base, making a right angle) is
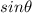 . The angle theta is opposite the
. The angle theta is opposite the
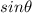 side.
side.
Explanation:
The pythagorean theorem applies to right triangles, which always have a 90 degree angle. Pythagorean identities are used to simplify trigonometric expressions/evaluate trig functions and to find the trig ratios in a right triangle.