Question

Where does Pythagorean identities and also how it relates to the right triangles

Answer 1

A pythagorean identity means that for any angle
`\theta`,
`sin^2\theta+cos^2\theta=1`.

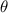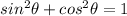This also means
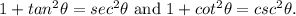`1+tan^2\theta=sec^2\theta \mbox{ and } 1+cot^2\theta=csc^2\theta.` The symbol, theta (
`\theta`) represents one of the acute angles in the right triangle. The hypotenuse (familiarly c in the regular pythagorean theorem) is 1. The triangle base is
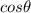`cos\theta`, and the height (side perpendicular to the base, making a right angle) is
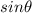`sin\theta`. The angle theta is opposite the
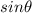`sin\theta` side.

Explanation:

The pythagorean theorem applies to right triangles, which always have a 90 degree angle. Pythagorean identities are used to simplify trigonometric expressions/evaluate trig functions and to find the trig ratios in a right triangle.

Answer 2

The Pythagorean identities are

`sin^(2) x + cos^(2) x = 1\\1+ tan^(2) x = sec^(2) x\\1 + cot^(2) x = csc^(2) x\\where\\csc x = (1)/(sinx) \\cot x = (cosx)/(sinx) or (1)/(tanx) \\tan x = (1)/(cotx) or (sinx)/(cosx) \\sec x = (1)/(cotx)`

No matter what the value of x (the angle degree amount) is, sin²x+cos²x is equal to 1

When given a side length of a right triangle you will be able to use one of these identities to find the angle amount