The equation we have is:
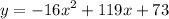
This is equation of a parabola that opens down.
To find the maximum point or the maximum height, we need to find the vertex of the parabola.
First, let's define variables:
A will be the coefficient of the x squared.
b is the coefficient of the x and
C is the independent term:
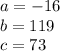
The vertex of will have the following x coordinate:
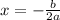
Substituting the values of a and b:
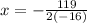
Solving the operations:

The next step is to substitute this x value into our equation to find the maximum height y:
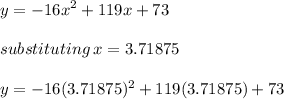
Solving the operations:
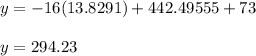
Rounding to the nearest tenth (1 decimal place)
y=294.2
Answer: 294.2 feet.