10x-16y=12 \\ 5x-3y=4 If (x, \ y) is a solution to the system of equations above, what is the value of x-y ?

Question

`10x-16y=12 \\ 5x-3y=4`

If
`(x, \ y)` is a solution to the system of equations above, what is the value of
`x-y` ?

Answer 1

`\displaystyle x-y=(24)/(25)`

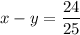
Explanation:

We are given the system:

`\left\{ \begin{array}{ll} 10x-16y=12 & \quad \\ 5x-3y=4& \quad \end{array} \right.`

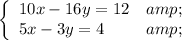
And asked to find the value of x - y if (x, y) is a solution to the above system.

Thus, let's solve the system. We can use eliminiation

We can see that the coefficients of x share a LCM.

Multiplying the second equation by negative two yields:

`\left\{ \begin{array}{ll} 10x-16y=12 & \quad \\ -10x+6y=-8 & \quad \end{array} \right.`

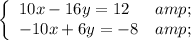
Adding the two equations yields:

`(10x-10x)+(-16y+6y)=(12+(-8))`

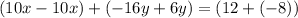
Simplify:

`-10y=4`

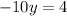
Solve for y:

`\displaystyle y = (4)/((-10)) = -(2)/(5)`

To find x, substitute y for either equation and evaluate. The second equation states that:

`5x-3y=4`

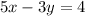
Substitute:

`\displaystyle 5x-3\left(-(2)/(5)\right)=4`

Multiply:

`\displaystyle 5x+(6)/(5)=4`

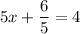
And solve for x:

`\displaystyle \begin{aligned} 5x+(6)/(5) &= 4 \\ \\ 5x &= (14)/(5) \\ \\ x &= (14)/(25)\end{aligned}`

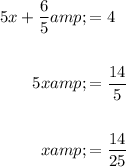
Hence, our solution to the system is:

`\displaystyle \left((14)/(25),- (2)/(5)\right)`

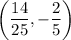
We want to find the value of:

`x-y`

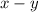
Substitute:

`\displaystyle = \left((14)/(25)\right) - \left(-(2)/(5)\right)`

Evaluate. Hence:

`\displaystyle x - y = (24)/(25)`

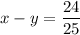
And we're done!

Answer 2

24/25

Explanation:

Step 1: Define systems of equation

10x - 16y = 12

5x - 3y = 4

Step 2: Rewrite one of the equations

5x = 4 + 3y

x = 4/5 + 3y/5

Step 3: Solve for y using Substitution

1. Substitute 2nd rewritten equation into 1: 10(4/5 + 3y/5) - 16y = 12
2. Distribute the 10 to both terms: 40/5 + 30y/5 - 16y = 12
3. Simplify the fractions down: 8 + 6y - 16y = 12
4. Combine like terms (y): 8 - 10y = 12
5. Subtract 8 on both sides: -10y = 4
6. Divide both sides by -10: y = 4/-10
7. Simply the fraction down: y = -2/5

Step 4: Substitute y back into an original equation to solve for x

1. Substitute: 5x - 3(-2/5) = 4
2. Multiply: 5x + 6/5 = 4
3. Subtract 6/5 on both sides: 5x = 14/5
4. Divide both sides by 5: x = 14/25

Step 5: Check to see if solution set (14/25, -2/5) is a solution.

1. Substitute into an original equation: 10(14/25) - 16(-2/5) = 12
2. Multiply each term: 28/5 + 32/5 = 12
3. Add: 12 = 12

Here, we see that x = 14/25, y = -2/5 and solution (14/25, -2/5) indeed works.

Step 6: Find x - y

x = 14/25

y = -2/5

1. Substitute: 14/25 - (-2/5)
2. Simplify (change signs): 14/25 + 2/5
3. Add: 24/25

Hope this helped! :)