Answer:
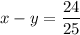
Explanation:
We are given the system:
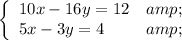
And asked to find the value of x - y if (x, y) is a solution to the above system.
Thus, let's solve the system. We can use eliminiation
We can see that the coefficients of x share a LCM.
Multiplying the second equation by negative two yields:
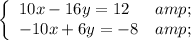
Adding the two equations yields:
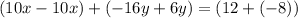
Simplify:
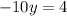
Solve for y:
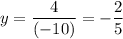
To find x, substitute y for either equation and evaluate. The second equation states that:
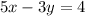
Substitute:
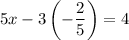
Multiply:
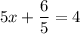
And solve for x:
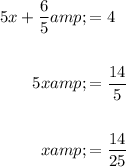
Hence, our solution to the system is:
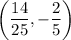
We want to find the value of:
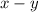
Substitute:
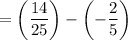
Evaluate. Hence:
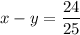
And we're done!