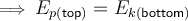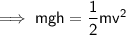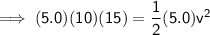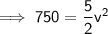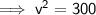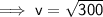Answer:
17.3 m/s (1 d.p.)
Step-by-step explanation:
Kinetic Energy

where:
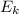 = kinetic energy in joules (J)
= kinetic energy in joules (J)- m = mass in kilograms (kg)
- v = speed in meters per second (m/s)
Gravitational potential energy
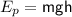
where:
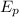 = gravitational potential energy in joules (J)
= gravitational potential energy in joules (J)- m = mass in kilograms (kg)
- g = gravitational field strength in newtons per kilogram (N/kg)
- h = change in height in meters (m)
Principle of Conservation of Energy
Gravitational potential energy at the top = kinetic energy at the bottom
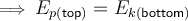
Given:
The gravitational field strength of the Earth is 10 N/kg (10 newtons per kilogram), therefore:
Substituting the values into the formula and solving for v: