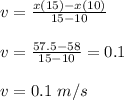Answer:
The answer is below
Step-by-step explanation:
Given that:
x(t) = at – bt2+c
a) x(t) = at – bt2+c
Substituting a = 1.4 m/s, b = 0.06 m/s2 and c =50 m gives:
x(t) = 1.4t - 0.06t² + 50
At t = 5, x(5) = 1.4(5) - 0.06(5)² + 50 = 55.5 m
At t = 0, x(0) = 1.4(0) - 0.06(0)² + 50 = 50 m
The average velocity (v) is given as:
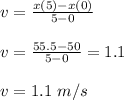
b) x(t) = 1.4t - 0.06t² + 50
At t = 10, x(10) = 1.4(10) - 0.06(10)² + 50 = 58 m
At t = 0, x(0) = 1.4(0) - 0.06(0)² + 50 = 50 m
The average velocity (v) is given as:
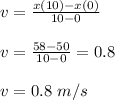
c) x(t) = 1.4t - 0.06t² + 50
At t = 15, x(5) = 1.4(15) - 0.06(15)² + 50 = 57.5 m
At t = 10, x(10) = 1.4(10) - 0.06(10)² + 50 = 58 m
The average velocity (v) is given as: