Explanation:
Let vertical height of ladder from ground be y and
horizontal distance of the base of the ladder from the wall be x respectively.
Length of the ladder = l (constant) = 10 ft
Using Pythagoras theorem:
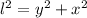
Differentiate both sides w.r.t time


We know that (After 1 sec, y = 6 ft and x = 8 ft ; dy/dt = 2 ft/sec)
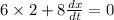
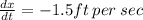
( Ignore - ive sign)
Therefore, bottom of the ladder is sliding away from the wall at a speed of 1.5 ft/sec one second after the ladder starts sliding.