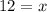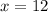Answer:
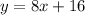
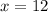
Explanation:
Given two points on the line (0, 16) and (3, 40), an equation for the line can be written using the slope-intercept line equation which takes the format
 .
.
Where,
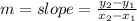
b = y-intercept or the point at which the line cuts the y-axis.
Let's find slope (m) using the slope formula:
Let,
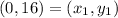
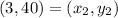
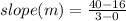
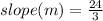
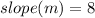
Find b. Substitute the values of x = 0, y = 16, and m = 8 in the slope-intercept formula to find b.


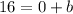
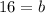
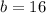
Plug in the values of m and b into the slope-intercept formula to get the equation of the line.

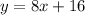
Let's use the equation to find x when y = 112.
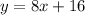
Substitute y = 112 in the equation

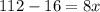
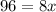
Divide both sides by 8