Answer:
The ratio of the mass of oxygen inhaled for each breath at this high altitude compared to that at sea level is 64.7 %
Step-by-step explanation:
Mass of air at sea level is given by;
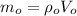
Mass of air at 14,200 ft altitude is given by;
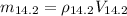
The ratio of the mass of oxygen at high altitude to that at sea level is given by;
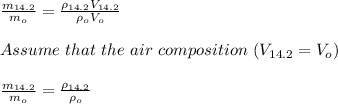
density of air at sea level,
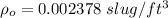
density of air at 10,000 ft = 0.001756 slug/ft³
density of air at 14,200 ft = x
density of air at 15,000 ft, = 0.001496 slug/ft³
Interpolate between 10,000 ft and 15,000 ft

The ratio of the mass of oxygen at 14,200 ft to that at sea level is given by;
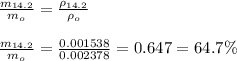
Therefore, the ratio of the mass of oxygen inhaled for each breath at this high altitude compared to that at sea level is 64.7 %